In Kahoots : EPR Paradox & Wave Particle Duality
- amuggs82
- Oct 12, 2024
- 4 min read
Updated: Dec 30, 2024
*A paradox situation where the roles of victim & oppressor, home & imprisonment, safety & danger are blurred & contradictory.

In quantum mechanics, the transformation of the superposition of particle mass to a particular region in a given location is typically achieved through the process of wave function collapse or measurement.
When a particle is in a superposition of states, its wave function represents all the possible states it can occupy simultaneously.
However, when a measurement is made, the wave function collapses to a single state corresponding to the outcome of the measurement.
In quantum mechanics how would you ‘transform’ or change the ‘superposition’ of particle mass to a particular region in a given location?
To confine the particle mass to a particular region in a given location, one can manipulate the environment or apply external fields to create localised potentials that effectively confine the particle within that region.
Reoccurring techniques that can be used to confine particles to specific regions;
Optical trapping
Magnetic trapping
Potential landscape manipulation
With the application of techniques such as quantum computing algorithms, quantum gates can be employed to manipulate quantum states and superpositions to perform specific tasks or computations.
These methods allow for controlling and transforming the quantum states of particles in a controlled manner.
Using the adequate dynamics (j,k,l) for ‘detection’ ie measurement of observables, in conjunction with Hilberts formalisation is it possible to achieve the change to ‘transformation’ ie ‘change of superposition’ of a single particle mass into a similar ‘state’ to a particular region in a given location using ?
In quantum mechanics, the transformation or change of superposition of a single particle mass into a particular region in a given location is fundamentally tied to the dynamics described by the Schrödinger equation & the principles of quantum mechanics, rather than being explicitly encoded in Hilbert space formalism alone.
Hilbert space formalism provides a mathematical framework to describe the state of quantum systems, where states are represented by vectors in a complex vector space. However, the transformation of superpositions involves the application of physical processes and interactions, which are usually described by the Schrödinger equation or other evolution equations in quantum mechanics.
The process of confining a particle to a particular region involves manipulating the potential energy landscape experienced by the particle. This can be achieved through techniques like applying external fields, creating barriers, or using traps to confine the particle within a desired region.
To achieve the transformation or change of superposition of a single particle mass into a particular region in a given location typically involves a combination of experimental techniques and theoretical modeling.
Here are some key steps & considerations:
1. Modeling the System:
Model the quantum system, including the potential landscape and the interactions that affect the particle’s motion and confinement. This involves specifying the Hamiltonian of the system, which describes the total energy of the particle and the potential energy due to the external fields or traps.
2. Designing Traps and Potentials:
Employ techniques such as optical trapping, magnetic trapping, or electrostatic trapping to create localised potentials that confine the particle within the desired region. These traps and potentials effectively shape the particle’s wave function, confining it spatially.
3. Applying External Fields:
Manipulate the external fields or potentials to guide the particle’s motion and shape its wave function according to the desired spatial distribution. This can involve adjusting the strengths & configurations of the trapping fields to achieve the desired confinement.
4. Time Evolution:
Allow the system to evolve over time according to the Schrödinger equation or other evolution equations in quantum mechanics. As the particle interacts with the trapping potentials and undergoes quantum dynamics, its wave function will evolve, potentially leading to the desired transformation from a superposition state to a localised state within the specified region.
5. Detection & Measurement:
Finally, perform measurements or detections to verify the success of the transformation. This could involve probing the particle’s position or other observables associated with its confinement within the region of interest.
While these steps provide a conceptual framework for achieving the transformation of superpositions to localised states, the specific implementation details and techniques can vary widely depending on the experimental setup and the properties of the particles involved.
Therefore, a combination of theoretical modeling and experimental techniques is typically required to achieve and verify such transformations in practice.
A simple example involving the trapping of a neutral atom using an optical dipole trap. The potential energy landscape experienced by the atom can be described by the following equation:
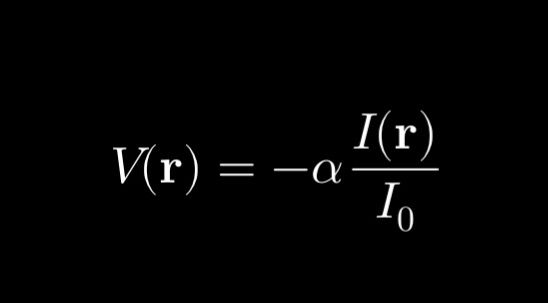
Where:
• is the potential energy at position .
• is the polarisability of the atom.
• is the intensity of the trapping laser at position .
• is the saturation intensity of the trapping laser.
The intensity distribution of the trapping laser can be controlled using optics, allowing for the creation of a desired potential landscape to confine the atom within a particular region.
The dynamics of the trapped atom can be described by the time-dependent Schrödinger equation:
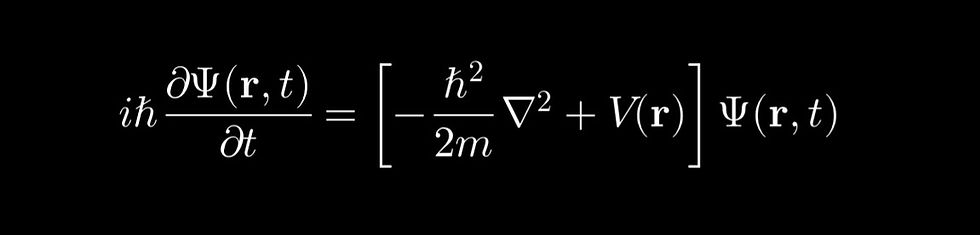
Where:
• is the wave function of the atom.
• is the mass of the atom.
• is the reduced Planck constant.
• is the Laplacian operator.
This equation governs the time evolution of the wavefunction of the trapped atom in the presence of the trapping potential .
To confine the atom within a specific region, one can design the intensity distribution of the trapping laser such that it creates a localised potential well where the atom is trapped. By solving the Schrödinger equation numerically or analytically, one can study the evolution of the atom’s wave function and its confinement within the trap.
Experimental techniques such as laser cooling and manipulation of the trapping laser’s parameters allow for precise control over the atom’s motion & confinement within the designed trap. Measurements of the atom’s position & other observables can then be performed to verify its confinement within the desired region.
This illustrates how theoretical formalisms such as the Schrödinger equation can be combined with experimental techniques to trap & confine particles within specific regions for various applications in quantum physics and quantum technology.
Comments